I’ve been researching quite a few algorithms for my client, Bruce, as I continue to scale out certain systems. I thought that getting them on my blog would be very useful for a future version of myself and many others. I suspect, and hope, that most folks that work in Systems Administration / Operations will find these at least familiar.

Flap Detection

Flap detection is the ability to determine rapid state changes so that one can take corrective action. The text book example is BGP route flapping where a new route is advertised and then withdrawn (a flap) multiple times in a short period. In general, this “scores” an event with higher scores the more frequent the event.

Warning: Math

For each event, a “penalty” $P$, “timestamp” $t$, and a boolean “isFlapping” variable is stored. $P$ is the current “score” for this event and is $0$ for an event that has not happened. $t$ is the timestamp, usually Unix Epoch time, of the last event.

Each time an event occurs we add a penalty value to the current penalty. The penalty value decays exponentially over time. A suppress limit is known which defines if the event is flapping when the event’s penalty is greater than the suppress limit. A lower reuse limit is known when the event is considered no longer flapping once the penalty value is less than the reuse limit.

Summary

Penalty	$P$	An event's current score.
Half-Life	$h$	How much time for half of the penalty to decay.
Timestamp	$t$	Unix Epoch time of last event.
Supress Limit		Penalty > Suppress Limit == Flapping
Reuse Limit		Penalty < Reuse Limit && Flapping == Recovery

Calculating for $P$

$$P(t_2) = P(t_1) \times e^{-(t_2 - t_1) \times ln(2) / h}$$

In Pictures

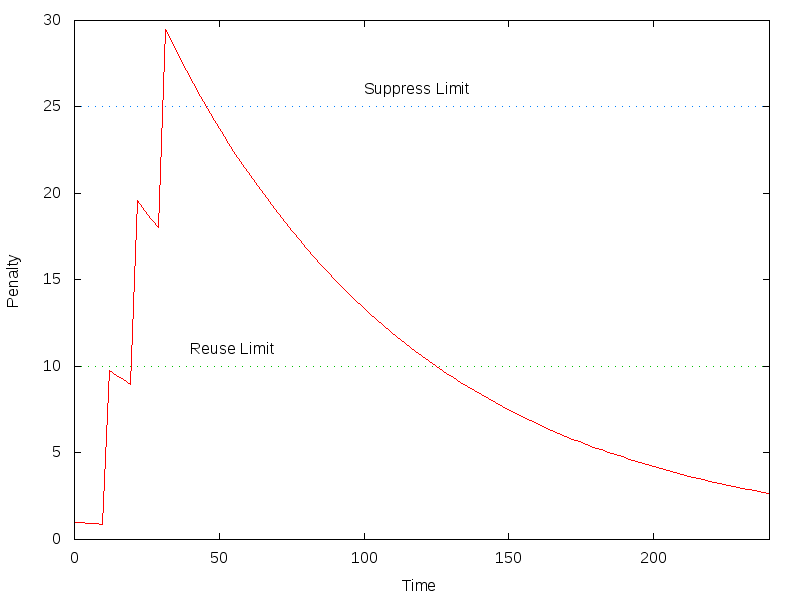
Notes

• This is not how Nagios does it.
• GNUPlot incantation:

f(x) = 2.71828 ** (-x*log(2) / 60)
set ylabel "Penalty"
set xlabel "Time"
set key off
set terminal png size 800,600
set output 'output.png'
set label "Reuse Limit" at 40,11
set label "Suppress Limit" at 100,26
plot [0:240] x < 10 ? f(x) : x < 20 ? f(x-10)*10 : x < 30 ? f(x-20)*20 : f(x-30)*30, 10 with dots, 25 with dots